“Fractals are not just artificial constructs, they shape us and the world we live in.” (Gleick – 1987).
Fractals for me, explain all natural phenomenon. While fractal geometry was conceived at the beginning of the 20th century, it was not until the advancement of the super computer that we have been able to see the complete implication and brilliance of fractals. I don’t claim to be an authority or expert on the subject, but I’ll try and explain here what little I know.
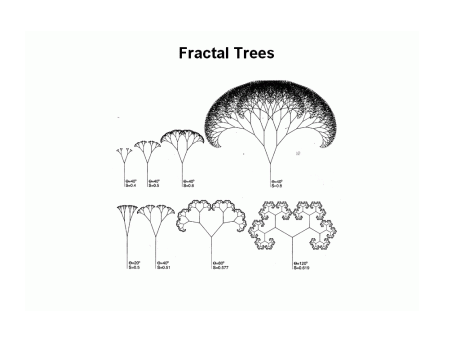
The notion behind fractals is moderately humble and apparent when described simply. But the arithmetic used to cultivate those concepts is not as easy. A fractal is a geometric figure with two distinct properties. Primarily, it is Irregular, fractured or fragmented. Moreover, it is Self-similar; that is, the figure appears similar no matter how great the scale of magnification. These objects display self-similar structure over an extended, but finite, scale range.
Alex Grey
Benoit Mandelbrot, now known as the ‘father or fractals’, devised the term fractal to define such figures, stemming from the Latin word “fractus” meaning broken, fragmented, or irregular. He also outlined astonishing parallels in appearance concerning some fractal sets and numerous natural geometric patterns. Consequently, the term “natural fractal” refers to natural phenomena that are similar to fractal sets, such as the path followed by a dust particle as it bounces about in the air.
“Fractal Geometry plays two roles. It is the geometry of deterministic chaos and it can also describe the geometry of mountains, clouds and galaxies.” – (Benoit Mandelbrot – 1984)
The majority of objects in nature do not adhere to simple traditional geometric forms. Clouds, trees, and mountains typically do not resemble circles, triangles, or squares. Within the natural world there are no straight lines or smooth edges. A sunflowers pattern for growth, the faultless symmetry of a microbe, the striped coat of a zebra, the barreling of ocean waves, or the harmonized turns and swoops of a flock of starlings twirling amongst trees prior to landing on a telephone wire. How can all those individuals part of the flock evade collisions or confrontations with their neighbors? How do they orchestrate these elegant, precise and instantaneous movements in such a sizeable group?These are a small number of thousands of additional examples are the kaleidoscope of patterns and forms that nature gifts us over a lifecycle.




Take a tree, for example. Preference a specific branch and examine it thoroughly. Then select a collection of leaves on that branch. In Chaology (the study of chaos) all three of the matters described – the tree, the branch, and the leaves – are identical. For many, the term chaos insinuates randomness, unpredictability and possibly even untidiness. Chaos is actually extremely structured and adheres to certain patterns and algorithms. The complications occur in finding these elusive and sophisticated patterns. One purpose of examining chaos through fractals is to grasp the patterns in the dynamical organization found in nature that superficially appear unpredictable and incomprehensible. To many Chaologists, the examination of chaos and fractals is beyond just an innovative and fresh field of science that fuses mathematics, theoretical physics, art, and computer science – it is a revolution. It is the breakthrough of a new geometry, one that helps us in defining and understanding the infinite universe we live in; one that is in constant motion, not as static depictions in textbooks. Today, fractal geometry has increasing implementations and applications, from predicting stock market prices to making new discoveries in theoretical physics.
Timm Dapper
Mathematicians have attempted to describe fractal shapes for over one hundred years, but with the processing power and imaging abilities of modern computers, fractals have enjoyed a new popularity because they can be digitally rendered and explored in all of their fascinating beauty. However beautiful these renderings are, for me they don’t compare to fractals that form in nature. Are visual intakes are saturated with the computer generated images representing fractals, so much so that for many they define fractal geometry. I feel that a reason for creating my video may be an attempt to disperse the brilliance of fractal geometry.
For a clear introduction to fractals (including an interesting fractal-generating application for Macintosh), go to:







[…] Fractals: The Blueprints for Chaos (orderinchoas.wordpress.com) […]